Class 10 Maths Ncert Solutions Triangles 6.3

Are you looking for the best Maths NCERT Solutions Chapter 6 Ex 6.3 Class 10? Then, grab them from our page and ace up your preparation for CBSE Class 10 Exams

Get Free NCERT Solutions for Class 10 Maths Chapter 6 Ex 6.3 PDF. Triangles Class 10 Maths NCERT Solutions are extremely helpful while doing your homework. Exercise 6.3 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 6 Maths Class 10 Triangles Exercise 6.3 provided in NCERT TextBook.

You can also download NCERT Solutions For Class 10 to help you to revise complete syllabus and score more marks in your examinations.

Free download NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.3 Triangles PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, AP SSC, TS SSC and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

• Triangles Class 10 Mind Map
• Triangles Class 10 Ex 6.1
• Triangles Class 10 Ex 6.1 in Hindi Medium
• Triangles Class 10 Ex 6.2
• Triangles Class 10 Ex 6.2 in Hindi Medium
• Triangles Class 10 Ex 6.3
• Triangles Class 10 Ex 6.3 in Hindi Medium
• Triangles Class 10 Ex 6.4
• Triangles Class 10 Ex 6.4 in Hindi Medium
• Triangles Class 10 Ex 6.5
• Triangles Class 10 Ex 6.5 in Hindi Medium
• Triangles Class 10 Ex 6.6
• Triangles Class 10 Ex 6.6 in Hindi Medium
• Extra Questions for Class 10 Maths Triangles
• Triangles Class 10 Notes Maths Chapter 6
• NCERT Exemplar Class 10 Maths Chapter 6 Triangles
• Important Questions for Class 10 Maths Chapter 6 Triangles

You can also download the free PDF of Ex 6.3 Class 10 Triangles NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 6
Chapter Name	Triangles
Exercise	Ex 6.3
Number of Questions Solved	16
Category	NCERT Solutions

NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.3

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex Ex 6.3 are part of Maths Class 10 NCERT Solutions. Here we have given NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.3

Question 1.
State which pairs of triangles in the given figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :


Solution:

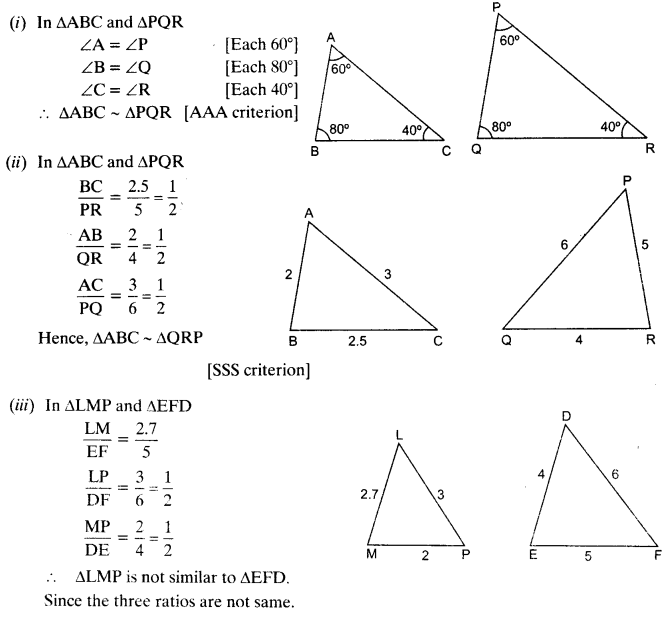
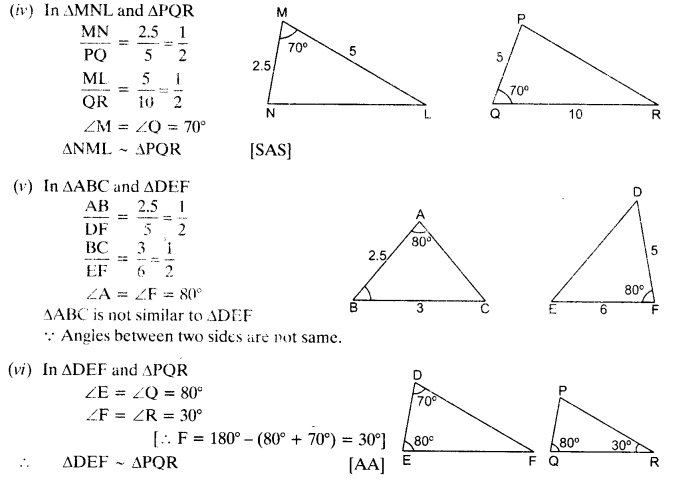
Question 2.
In the given figure, ∆ODC ~ ∆OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
Solution:

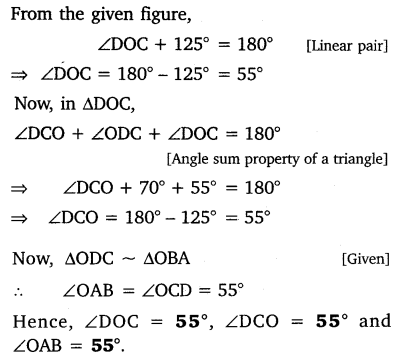
Download NCERT Solutions For Class 10 Maths Chapter 6 Triangles PDF

Question 3.
Diagonals AC and BD of a trape∠ium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \(\frac { OA }{ OC } =\frac { OB }{ OD^{ \bullet } } \)
Solution:

Question 4.
In the given figure, \(\frac { QR }{ QS } =\frac { QT }{ PR } \) and ∠1 = ∠2. show that ∆PQR ~ ∆TQR.
Solution:

Question 5.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:

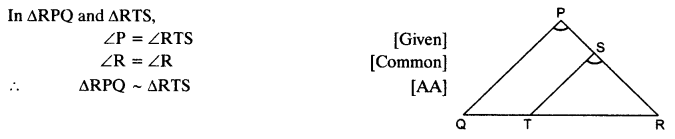
Question 6.
In the given figure, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.
Solution:

Question 7.
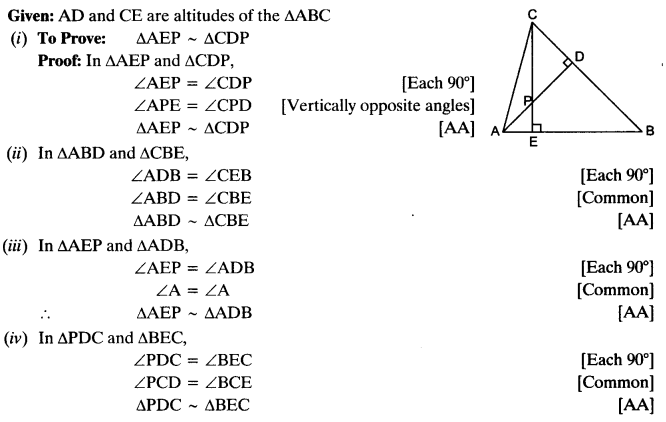
In the given figure, altitudes AD and CE of ∆ABC intersect each other at the point P. Show that:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
Solution:

Question 8.
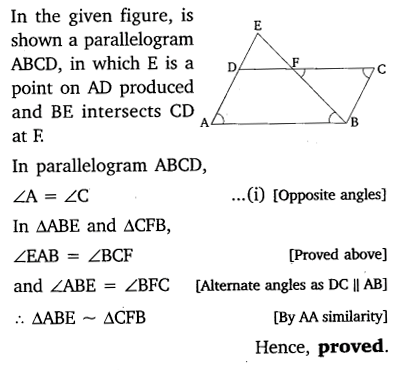
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:

Question 9.
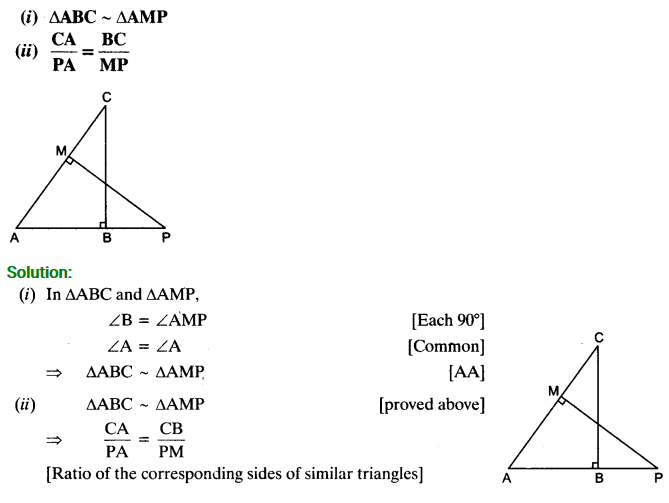
In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

Solution:

Question 10.
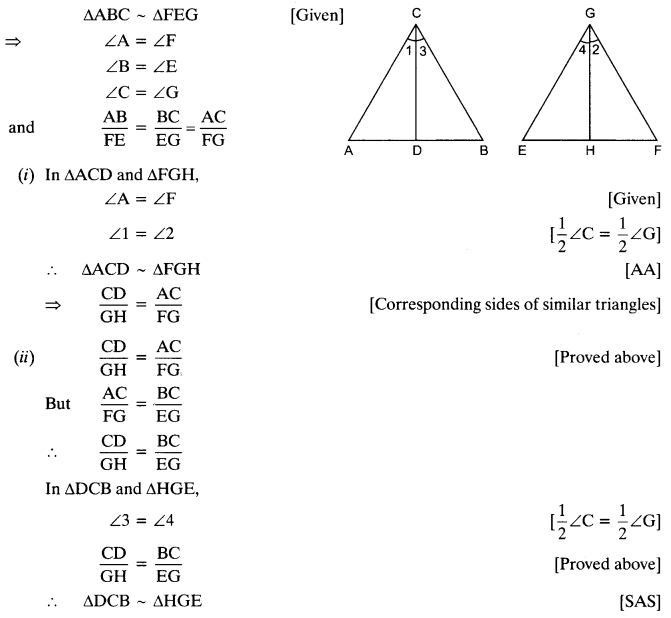
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that

Solution:

Question 11.
In the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ABD ~ ∆ECF.
Solution:

Question 12.
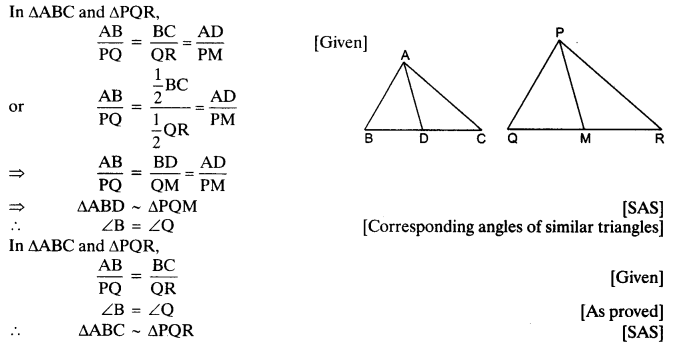
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR (see in given figure). Show that ∆ABC ~ ∆bPQR.
Solution:

Question 13.
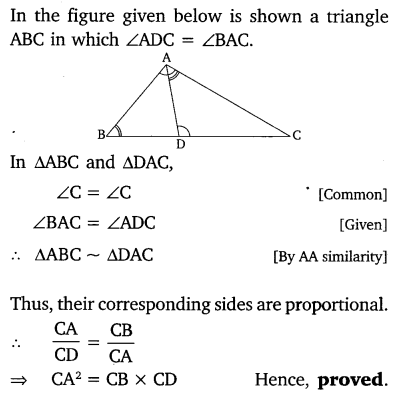
D is a point on the side BC of a triangle ABC, such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Solution:

Question 14.
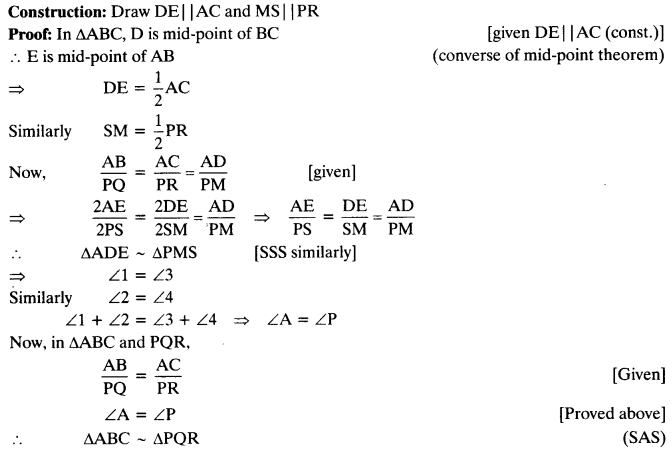
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution:

Question 15.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:

Question 16.
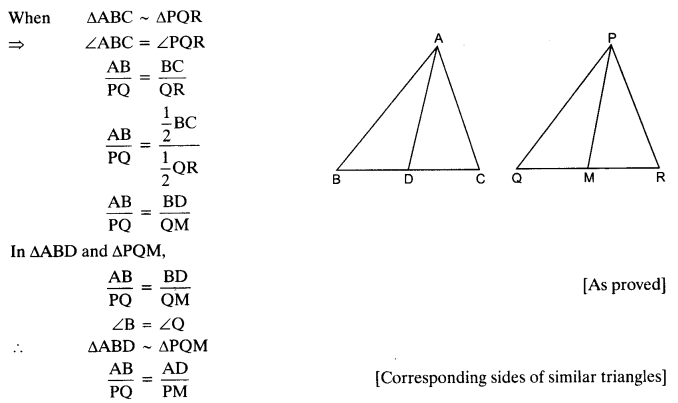
If AD and PM are medians of triangles ABC and PQR respectively, where
∆ABC ~ ∆PQR. Prove that \(\frac { AB }{ PQ } =\frac { AD }{ P{ M }^{ \bullet } } \)
Solution:

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3 in Hindi Medium

Q1. बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कौन – कौन से युग्म समरूप हैं | उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देनें में किया है तथा साथ ही समरूप  त्रिभुजों को सांकेतिक रूप  में व्यक्त कीजिए |

हल : (i)

ΔABC तथा ΔPQR में

∠ABC = ∠PQR = 80°

∠BAC = ∠QPR = 60°

∠ACB = ∠PRQ = 40°

∴ AAA समरूपता कसौटी से

ΔABC ~ ΔPQR

हल : (ii)

हल : (iii)

त्रिभुजों का यह युग्म समरूप नहीं है |

हल : (iv)

त्रिभुजों का यह युग्म समरूप नहीं है |

हल : (v)

त्रिभुजों का यह युग्म समरूप नहीं है |

हल : (vi)

Q2. आकृति 6.35 में, ΔODC ~ ΔOBA, ∠BOC = 125^oऔर ∠CDO = 70^o है | ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए |

हल :∠DOC + ∠BOC = 180°  (रैखिक युग्म)

⇒ ∠DOC +125^o = 180°

⇒ ∠DOC = 180° -125^o

⇒ ∠DOC = 55^o

अब ΔDOC  में,

∠DOC + ∠CDO + ∠DCO = 180°   (त्रिभुज के तीनों कोणों का योग)

⇒ 55^o + 70^o + ∠DCO = 180°

⇒ 125^o ∠DCO = 180°

⇒ ∠DCO = 180° – 125^o

⇒ ∠DCO = 55^o

ΔODC ~ ΔOBA (दिया है)

∴ ∠OAB = ∠DCO = 55^o

समरूप त्रिभुज के संगत कोण बराबर होते हैं|)

​Q3. समलंब ABCD, जिसमे AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए,

Q5. D PQR की भुजाओं PR और QR पर क्रमश: बिंदु S और T इस प्रकार स्थित हैं कि∠P  =∠RTS है | दर्शाइए किΔRPQ ~ ΔRTS  है |

हल:

दिया है : DPQR की भुजाओं PR और QR पर

क्रमश: बिंदु S और T इस प्रकार स्थित हैं

कि ∠P = ∠RTS है |

सिद्ध करना है : ΔRPQ~ ΔRTS

प्रमाण : ΔRPQ तथा ΔRTS में,

∠P = ∠RTS   (दिया है )

∠R = ∠R      (उभयनिष्ठ)

A.A समरूपता कसौटी से

ΔRPQ~ ΔRTS

Q6. आकृति 6.37 में, यदिΔABE ≅ ΔACD है, तो दर्शाइए किΔADE ~ ΔABCहै |

Q7. आकृति 6.38 में, DABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं तो दर्शाइए कि :

(i) Δ AEP ~ Δ CDP
(ii) Δ ABD ~ Δ CBE
(iii) Δ AEP ~ Δ ADB
(iv) Δ PDC ~ Δ BEC

हल:

दिया है : DABC के शीर्षलंब AD और CE परस्पर बिंदु P पर प्रतिच्छेद करते हैं |

सिद्ध करना है :

(i) Δ AEP ~ Δ CDP
(ii) Δ ABD ~ Δ CBE
(iii) Δ AEP ~ Δ ADB
(iv) Δ PDC ~ Δ BEC

प्रमाण :

(i)  Δ AEP तथा Δ CDP में,

∠AEP = ∠CDP  (प्रत्येक 90°)

∠APE = ∠CPD  (शीर्षाभिमुख कोण)

A.A समरूपता कसौटी से

Δ AEP ~ Δ CDP

(ii) Δ ABD तथा CBE में

∠ADB = ∠CEB  (प्रत्येक 90°)

∠B = ∠B     (उभयनिष्ठ)

A.A समरूपता कसौटी से

Δ ABD ~ Δ CBE

(iii)  Δ AEP तथा Δ ADB में

∠AEP = ∠ADB  (प्रत्येक 90°)

∠A = ∠A     (उभयनिष्ठ)

A.A समरूपता कसौटी से

Δ AEP ~ Δ ADB

(iv) Δ PDC तथा Δ BEC में

∠PDC = ∠BEC  (प्रत्येक 90°)

∠C = ∠C     (उभयनिष्ठ)

A.A समरूपता कसौटी से

Δ PDC ~ Δ BEC

Q8. समान्तर चतुर्भुज ABCD की बढाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है | दर्शाइए कि Δ ABE  ~ Δ CFB है |

हल:

दिया है : ABCD एक समान्तर चतुर्भुज है जिसकी बढाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है |

सिद्ध करना है : Δ ABE ~ Δ CFB

प्रमाण : ABCD एक समान्तर चतुर्भुज है |

∠AEB = ∠CBE  …. (1) एकान्तर कोण

Δ ABE तथा Δ CFB में,

∠AEB = ∠CBE  समी० (1) से

∠A = ∠C  (समांतर चतुर्भुज के सम्मुख कोण)

A.A समरूपता कसौटी से

Δ ABE ~ Δ CFB

Q9. आकृति 6.39 में, ABC और AMP दो समकोण त्रिभुज है, जिसके कोण B और M समकोण हैं | सिद्ध कीजिए कि :

(i) Δ ABC  ~ Δ AMP

हल:

दिया है  :ABC और AMP दो समकोण त्रिभुज है, जिसके कोण B और M समकोण हैं |

सिद्ध करना है :

(i) Δ ABC ~ Δ AMP

प्रमाण :

(i)     Δ ABC तथा Δ AMP में

∠ABC = ∠AMP  (प्रत्येक 90°)

∠A = ∠A     (उभयनिष्ठ)

A.A समरूपता कसौटी से

Δ ABC ~ Δ AMP

(चूँकि समरूप त्रिभुज के संगत भुजाएँ समानुपाती होतीं हैं |)

Q10. CD और GH क्रमश: ∠  ACB और ∠  EGF  के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमश: Δ ABC और Δ FEG की भुजाओं AB और FE पर स्थित हैं | यदि Δ ABC ~ Δ FEG है, तो दर्शाइए कि :

(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF

हल:

दिया है  :CD और GH क्रमश: ∠ ACB  और ∠ EGF के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमश: Δ ABC और ΔFEG की भुजाओं AB और FE पर स्थित हैं और ΔABC ~ ΔFEG है |

(समरूप त्रिभुज के संगत कोण बराबर होते हैं |)

(i)     Δ ABC तथा Δ AMP में

(ii)  Δ DCB तथा Δ HGE में,

∠B = ∠E  समी० (2) से

∠BCD = ∠EGH  [चूँकि  ½∠C = ½∠G समी० (3) से ]

A.A समरूपता कसौटी से

Δ DCB ~ Δ HGE

(iii) Δ DCA तथा Δ HGF में
∠A = ∠F  समी० (1) से

∠ACD = ∠FGH  [चूँकि  ½∠C = ½∠G समी० (3) से ]

A.A समरूपता कसौटी से

Δ DCA ~ Δ HGFProved

Q11.आकृति 6.40 में , AB = AC वाले , एक समद्विबाहु त्रिभुज ABC की बढाई गई भुजा CBपर स्थित E एक बिन्दु है | यदि AD ⊥ BC और EF ⊥ AC है तो सिद्ध कीजिए कि Δ ABD ~ Δ ECF है |

हल:

दिया है  :AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढाई गई भुजा CB पर स्थित E एक बिन्दु है जिसमें AD ⊥ BC और EF ⊥ AC है

सिद्ध करना है :

ΔABD ~ ΔECF

प्रमाण :

ΔABC में,

AB = AC दिया है;

∴ ∠B = ∠C    ……… (1) (बराबर भुजाओं के सम्मुख कोण ….)

अब, ΔABD तथा ΔECF में

∠ADB = ∠EFC (प्रत्येक 90°)

∠B = ∠C    समी० (1) से

A.A समरूपता कसौटी से

ΔABD ~ ΔECF    Proved

Q12 . एक त्रिभुज ABC कि भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं (देखिए आकृति 6.41)|दर्शाइए कि Δ ABC ~ Δ PQR है |

हल:

दिया है  :त्रिभुज ABC कि भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं |

सिद्ध करना है :

ΔABC ~ ΔPQR

(चूँकि माध्यिकाएँ AD तथा PM BC तथा QR को समद्विभाजित करती हैं |)

Q13. एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ ADC = ∠ BAC है | दर्शाइए कि CA²= CB.CD है |

हल :

दिया है : त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है |

सिद्ध करना है : CA²= CB.CD

प्रमाण :

अब, ΔADC तथा ΔBAC में

∠ADC = ∠BAC ( दिया है )

∠C = ∠C    (उभयनिष्ठ)

A.A समरूपता कसौटी से

ΔADC ~ ΔBAC

(चूँकि समरूप त्रिभुज के संगत भुजाएँ समानुपाती होतीं हैं |)

या   CA²= CB.CD  (बाई-क्रॉस गुणा करने पर)

Proved

Q14. एक त्रिभुज ABC की  भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं | दर्शाइए कि Δ ABC ~ Δ PQR है |

हल :

यहाँ माध्यिकाएँ समान अनुपात में हैं इसलिए समान अनुपात की माध्यिकायें जिस भुजा को समद्विभाजित करती है वह भी समानुपाती होता है

Q15. लंबाई 6m वाले एक उध्वार्धर स्तम्भ की भूमि पर छाया की लंबाई 4m है , जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है | मीनार की ऊँचाई ज्ञात कीजिए |

We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.3, drop a comment below and we will get back to you at the earliest.

Class 10 Maths Ncert Solutions Triangles 6.3

Source: https://www.learncbse.in/ncert-solutions-for-class-10-maths-chapter-6-ex-6-3/

Share this post